Here is another GED Math practice test that allows the use of a calculator. The majority of the GED 2024 Math questions do allow using a calculator. As you work through these problems, be sure to review the explanations for any wrong answers. It is very important to learn from your mistakes!
Directions: Solve each problem and select the best answer. You may use your calculator. You may also refer to the GED Formula Sheet as needed.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
At a local yoga studio, 80% of the members are women and 20% of the members are men. The average age of the women is 30 and the average age of the men is 40. What is the average age of all the members?
30 | |
32 | |
33 | |
35 |
Question 1 Explanation:
This is a weighted average problem, in which the average age of the women carries a weight of 80% and the average age of the men carries a weight of 20%. The combined average age will be the sum of the contribution of each group; which is found by multiplying the group’s average by its weight.
Begin by finding the women’s contribution to the overall average (recall that 80% = 0.8): 0.8 * 30 = 24
Next, find the men’s contribution: 0.2 * 40 = 8
Combine these to find the overall average: 24 + 8 = 32
Notice that this combined average is between the average age of the women (30) and the average age of the men (40), which makes sense because both groups are contributing to the overall average.
Begin by finding the women’s contribution to the overall average (recall that 80% = 0.8): 0.8 * 30 = 24
Next, find the men’s contribution: 0.2 * 40 = 8
Combine these to find the overall average: 24 + 8 = 32
Notice that this combined average is between the average age of the women (30) and the average age of the men (40), which makes sense because both groups are contributing to the overall average.
Question 2 |
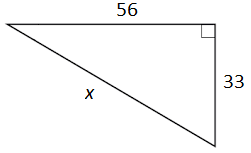
Calculate the value of x for the right triangle shown below.
66 | |
89 | |
56 | |
65 |
Question 2 Explanation:
The Pythagorean theorem can be used to find the missing segment of a right triangle. This is one of the formulas given on the GED Formula Sheet. The theorem relates the legs of a right triangle to its hypotenuse as a² + b² = c², where a and b are the legs and c is the hypotenuse. The hypotenuse is the longest side in a right triangle and is always opposite the right angle.
Substitute the known values into their appropriate places and solve for the unknown side length:
33² + 56² = c²
Evaluate the squares:
1,089 + 3,136 = c²
4,225 = c²
Evaluate the square root of both sides:
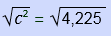
c = 65
Substitute the known values into their appropriate places and solve for the unknown side length:
33² + 56² = c²
Evaluate the squares:
1,089 + 3,136 = c²
4,225 = c²
Evaluate the square root of both sides:
c = 65
Question 3 |
Each player on the high school football team has been weighed, and the data are shown in the box-and-whisker plot below.
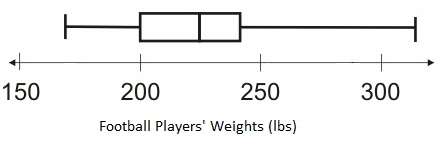
Based on this box-and-whisker plot, which of the following statements is accurate?
The heaviest player weighs 300 lbs. | |
One-fourth of the players weigh less than 200 lbs. | |
The median player weighs 245 lbs. | |
The lightest player weighs 200 lbs. |
Question 3 Explanation:
The ability to interpret data from a box-and-whisker plot is a required skill for the GED Math test. Here is the meaning of each part of the box-and-whisker plot:
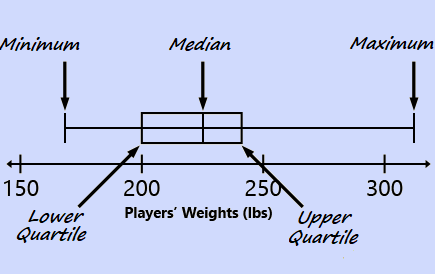
In this example, the minimum value represents the lightest player on the team and the maximum value represents the heaviest player on the team. The median value is the player who is at the midpoint of the distribution. The quartile values divide the distribution into fourths. Since the lower quartile is at 200, it is accurate to say that one-fourth of the players weigh less than 200 lbs.

In this example, the minimum value represents the lightest player on the team and the maximum value represents the heaviest player on the team. The median value is the player who is at the midpoint of the distribution. The quartile values divide the distribution into fourths. Since the lower quartile is at 200, it is accurate to say that one-fourth of the players weigh less than 200 lbs.
Question 4 |
Each time they play a game there is a 90% chance that the Blue Comets soccer team will score the first goal. What is the probability of the Blue Comets scoring the first goal in 4 straight games?
0.81 | |
0.45 | |
0.729 | |
0.656 |
Question 4 Explanation:
First recognize that the probability of the Blue Comets scoring the first goal in any single game is 90% regardless of whether they score first in any other game. This indicates that scoring first in consecutive games are independent events. To find the probability of consecutive independent events occurring, calculate the product of their probabilities.
The probability of the team scoring first in 4 straight games is then:
0.9 * 0.9 * 0.9 * 0.9 = 0.6561, which rounds to 0.656.
The probability of the team scoring first in 4 straight games is then:
0.9 * 0.9 * 0.9 * 0.9 = 0.6561, which rounds to 0.656.
Question 5 |
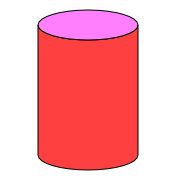
Calculate the surface area of this soup can. The height of the can is 6 inches and the diameter of the lid is 3 inches.
14.13 in² | |
56.52 in² | |
70.65 in² | |
169.56 in² |
Question 5 Explanation:
To solve this you can use the equation for the surface area of a cylinder. This is one of the equations provided on the GED Formula Sheet:
SA = 2πrh + 2πr²
Recall that π (pi) is approximately equal to 3.14. We have the diameter of the lid, but we need the radius. The radius is equal to half the diameter, so r = 1.5 in. The height is given as h = 6 in:
SA = 2(3.14)(1.5)(6) + 2(3.14)(1.5)²
Use your calculator to solve. Remember your order of operations. Calculate the exponent first, followed by the multiplication, and then the addition:
SA = 2(3.14)(1.5)(6) + 2(3.14)(2.25)
SA = 56.52 + 14.13
SA = 70.65 in²
SA = 2πrh + 2πr²
Recall that π (pi) is approximately equal to 3.14. We have the diameter of the lid, but we need the radius. The radius is equal to half the diameter, so r = 1.5 in. The height is given as h = 6 in:
SA = 2(3.14)(1.5)(6) + 2(3.14)(1.5)²
Use your calculator to solve. Remember your order of operations. Calculate the exponent first, followed by the multiplication, and then the addition:
SA = 2(3.14)(1.5)(6) + 2(3.14)(2.25)
SA = 56.52 + 14.13
SA = 70.65 in²
Question 6 |
Charlie lives halfway between Chicago and Hoopertown. Amanda lives halfway between Charlie and Chicago. Raymond lives between Charlie and Hoopertown. All three houses lie on a straight line from Chicago to Hoopertown.
If Raymond lives 15 miles from Amanda and 23 miles from Chicago, how far does he live from Hoopertown?
5 Miles | |
7 Miles | |
9 Miles | |
12 Miles |
Question 6 Explanation:
Draw a diagram, and label all of the given information to help you solve this problem. Use the provided relationships to solve for the unknown distances.
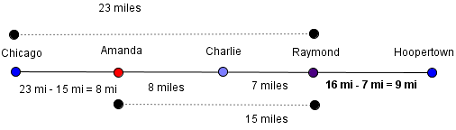
The given information tells us that Raymond lives 15 miles from Amanda and 23 miles from Chicago. Subtract these quantities to find the distance from Amanda’s house to Chicago: 23 − 15 = 8 miles. Amanda lives halfway between Charlie and Chicago, so the distance between her house and Charlie’s is 8 miles. The distance from Charlie’s house to Chicago is 8 + 8 = 16 miles. If Charlie lives 16 miles from Chicago and Raymond lives 23 miles from Chicago, then the distance between their houses must be 23 − 16 = 7.
Since Charlie’s house is equidistant from Chicago and Hoopertown, the distance from Charlie’s to Hoopertown must also be 16 miles. Raymond lives 7 miles from Charlie so the distance from Raymond’s house to Hoopertown is 16 − 7 = 9 miles.

The given information tells us that Raymond lives 15 miles from Amanda and 23 miles from Chicago. Subtract these quantities to find the distance from Amanda’s house to Chicago: 23 − 15 = 8 miles. Amanda lives halfway between Charlie and Chicago, so the distance between her house and Charlie’s is 8 miles. The distance from Charlie’s house to Chicago is 8 + 8 = 16 miles. If Charlie lives 16 miles from Chicago and Raymond lives 23 miles from Chicago, then the distance between their houses must be 23 − 16 = 7.
Since Charlie’s house is equidistant from Chicago and Hoopertown, the distance from Charlie’s to Hoopertown must also be 16 miles. Raymond lives 7 miles from Charlie so the distance from Raymond’s house to Hoopertown is 16 − 7 = 9 miles.
Question 7 |
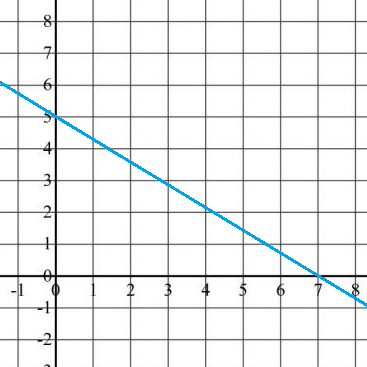
What is the slope of the line that passes through points (0,5) and (7,0) on the coordinate plane shown below?
Question 7 Explanation:
The slope of a line, which can be remembered as “the rise over the run,” is the change in y values divided by the change in x values across two points on a line. The slope is defined as:
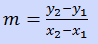
Substitute the given points (0,5) and (7,0) into the equation to calculate the slope:
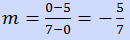
Substitute the given points (0,5) and (7,0) into the equation to calculate the slope:
Question 8 |
Which of the following equations represents y in terms of x for all ordered pairs listed?
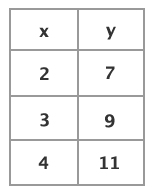
y = 4x ÷ 3 | |
y = 2x + 3 | |
y = x + 5 | |
y = 3x2 |
Question 8 Explanation:
By inspecting the ordered pairs, it can be seen that as the x value increases by 1, the y value increases by 2. This indicates a linear relationship, and the answer choice containing x2 can be eliminated. Using the definition of the slope, which is calculated as:
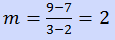
The answer must be y = 2x + 3. This answer can be further verified by substituting each ordered pair into the equation, for example:
11 = 2(4) + 3
11 = 8 + 3
11 = 11
The answer must be y = 2x + 3. This answer can be further verified by substituting each ordered pair into the equation, for example:
11 = 2(4) + 3
11 = 8 + 3
11 = 11
Question 9 |
If x is a small negative integer and y is a large positive integer, which of the following expressions must be positive?
x * y | |
y − x | |
y ÷ x | |
x ÷ y |
Question 9 Explanation:
Before considering the answer choices, recall the properties of positive and negative integers. Both multiplication and division of a positive integer with a negative integer always yield a negative integer. Consequently, the only possible answer choice that must be positive is y − x.
An alternative solution is choosing a small negative integer for x, −1, and a large positive integer for y, 100, and substituting these values into each of the answer choices.
An alternative solution is choosing a small negative integer for x, −1, and a large positive integer for y, 100, and substituting these values into each of the answer choices.
Question 10 |
Li wants to buy as many bags of mulch as possible with his $305, and he would like them to be delivered to his house. The cost is $7.50 per bag and there is a $35.75 delivery charge. The mulch is only sold in full bags. How many bags can Li buy?
35 | |
36 | |
45 | |
46 |
Question 10 Explanation:
From Li’s initial amount of $305, a flat $35.75 delivery charge is deducted:
$305 − $35.75 = $269.25.
We can then divide this amount by the cost per bag to find the total number of bags that Li can buy:
$269.25 ÷ $7.50 = 35.9 bags. However, the question states that the mulch can only be sold in full bags, so we must round our answer down to ensure that Li does not exceed his budget.
$305 − $35.75 = $269.25.
We can then divide this amount by the cost per bag to find the total number of bags that Li can buy:
$269.25 ÷ $7.50 = 35.9 bags. However, the question states that the mulch can only be sold in full bags, so we must round our answer down to ensure that Li does not exceed his budget.
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 10 questions to complete.
|
List |
More GED Practice:
GED Math Practice Test 4 >>