This is the first of our free GED Math practice tests, and it has been fully updated to reflect the latest 2024 GED revisions. To prepare for your GED Math test you will want to work through as many practice questions as possible. After answering each of these questions, the correct answer will be provided along with a detailed explanation. Get started on your test prep right now with this GED Math practice test.
Directions: Solve each problem and select the best answer. You may use your calculator. You may also refer to the GED Formula Sheet as needed.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Devon owns a house cleaning company and has to give price quotes to potential customers. He figures out his price by assuming a $25 base charge and then adding $8 for each bathroom and $4 for each other room.
If he uses P to represent the price, B for bathroom, and R for other rooms, which of the following represents his price quote formula?
P = 25 + 12(BR) | |
P = 25 + 8B + 4R | |
P = 25(4R + 8B) | |
P = (4)(8)(R + B) + 25 |
Question 1 Explanation:
The price quote, P, will be equal to the total amount of charges. It’s given that there is a $25 base charge, so we can begin by writing the price quote as P = $25. To this base charge of $25, $8 per each bathroom, represented by the variable B, is added; our price quote is now P = $25 + $8B. Lastly, $4 per each other room, R, is added, and the actual price quote is P = $25 + $8B + $4R, or P = 25 + 8B + 4R.
Question 2 |
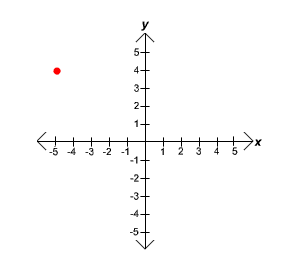
What are the coordinates of the point shown on this coordinate plane?
(5, −5) | |
(4, −5) | |
(−5, 4) | |
(5, −4) |
Question 2 Explanation:
The coordinate plane is formed by a horizontal x-axis and a vertical y-axis that intersect at the origin, represented as (0, 0). Points on the plane have both an x coordinate and a y coordinate and are written in the form (x, y). Negative x values are to the left of the origin, positive x values are to the right of the origin; negative y values are below the origin, and positive y values are above the origin. In this case, the point is to the left and above the origin. The only answer choice containing a negative x coordinate must be correct.
Question 3 |
Given f(x) = 2x2 − 3x + 7, find f(2.5)
5 | |
12 | |
19 | |
24.5 |
Question 3 Explanation:
This is a function problem. A function relates an input to an output. To find ƒ(2.5), substitute 2.5 for every x in the original function and evaluate the expression:
ƒ(2.5) = 2(2.5)2 − 3(2.5) +7
ƒ(2.5) = 2(6.25) − 7.5 + 7
ƒ(2.5) = 12.5 − 7.5 + 7
ƒ(2.5) = 12
ƒ(2.5) = 2(2.5)2 − 3(2.5) +7
ƒ(2.5) = 2(6.25) − 7.5 + 7
ƒ(2.5) = 12.5 − 7.5 + 7
ƒ(2.5) = 12
Question 4 |
Solve 5x + 8 < 3(x + 2)
x < −1 | |
x < −3 | |
x > 1 | |
x > −¾ |
Question 4 Explanation:
In order to solve inequalities in one variable, follow the order of operations (PEMDAS) to simplify the expressions, then combine like terms, then isolate the variable. Inequalities can be treated much like equations, but with one major difference: when multiplying or dividing either side of an inequality by a negative value, the direction of the inequality symbol must switch.
In this case, begin by multiplying the 3 through the parentheses, before then isolating the variable:
5x + 8 < 3(x + 2)
5x + 8 < 3x + 6
2x + 8 < 6
2x < −2
x < −1
In this case, begin by multiplying the 3 through the parentheses, before then isolating the variable:
5x + 8 < 3(x + 2)
5x + 8 < 3x + 6
2x + 8 < 6
2x < −2
x < −1
Question 5 |
Simplify (x6)(x5)
2x11 | |
2x30 | |
x11 | |
x30 |
Question 5 Explanation:
Recall that the multiplication of terms sharing the same base can be simplified by adding the exponents: xa * xb = x(a + b). If this rule is forgotten, you can quickly derive it by considering the simple case of 21 * 22, which can be rewritten as 2 * 2 * 2, or 23. The expression in this case, then, can be simplified as:
(x6) (x5) = x5+6
= x11
(x6) (x5) = x5+6
= x11
Question 6 |
The area of the circle shown below is 100π. What is the diameter (D) of the circle?
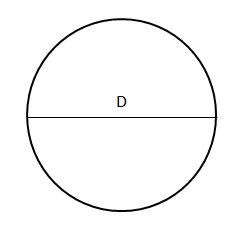
10 | |
20 | |
30 | |
40 |
Question 6 Explanation:
Begin by writing out the formula for the area of a circle, which is one of the formulas provided on the GED Formula Sheet. Next, substitute the given value for the area, and then solve for the radius. Recall that the square root of both sides must be evaluated in order to isolate r. Multiplying the value of r by 2 gives the diameter:
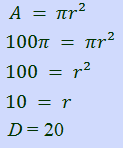
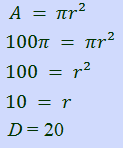
Question 7 |
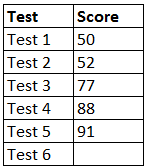
Max struggled with his math class early in the year, but he has been working hard to improve his scores. There is one test left, and he is hoping that his final average test score will be 75. What score will he need to get on Test 6 to finish the year with an average score of 75?
75 | |
85 | |
92 | |
100 |
Question 7 Explanation:
The average of a set of data points is the sum of the data points divided by the total number of data points. In this case, we are given 5 out of 6 data points, the number of data points, and the desired average. Substitute the given values into the formula for the average, using a variable to represent the unknown test score, and then solve for the variable:
Average = sum of data points ÷ number of data points
75 = (50 + 52 + 77 + 88 + 91 + x) ÷ 6
Now solve for x. Start with the addition:
75 = (358 + x) ÷ 6
Next, eliminate the denominator by multiplying both sides by 6:
450 = 358 + x
The last step is to subtract 358 from both sides:
x = 92
Average = sum of data points ÷ number of data points
75 = (50 + 52 + 77 + 88 + 91 + x) ÷ 6
Now solve for x. Start with the addition:
75 = (358 + x) ÷ 6
Next, eliminate the denominator by multiplying both sides by 6:
450 = 358 + x
The last step is to subtract 358 from both sides:
x = 92
Question 8 |
If a = −4, and b = 3, what is |a − b|?
1 | |
3 | |
4 | |
7 |
Question 8 Explanation:
The vertical bars surrounding a − b designate the absolute value of the difference. The absolute value of an expression is the distance from the simplified expression to 0; absolute value is always positive. Substitute the given values of a and b into the expression, evaluate the difference, and then apply the absolute value to make it positive.
|a − b|
= |−4 − 3|
= |−7| = 7
Recall that −4 − 3 is equivalent to −4 + −3 = −7
|a − b|
= |−4 − 3|
= |−7| = 7
Recall that −4 − 3 is equivalent to −4 + −3 = −7
Question 9 |
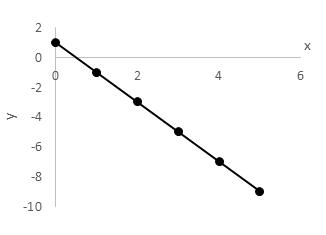
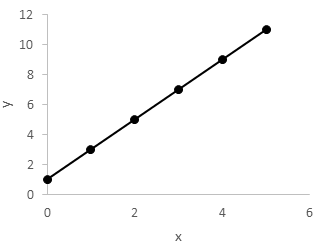
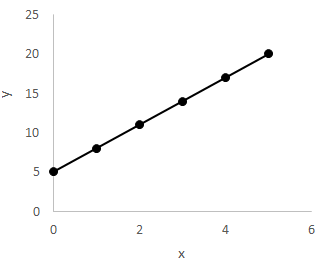
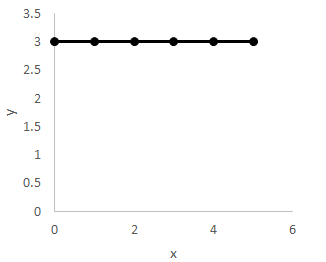
Which of the following graphs represents the equation y = 2x + 1?
 | |
 | |
 | |
 |
Question 9 Explanation:
An equation of the form y = ax + b, where a and b are constants, designates a straight line and is known as the slope-intercept form of the line because it explicitly provides both the slope and y-intercept. The variable a represents the slope of the line, which can be negative, zero, positive, or undefined; the variable b represents the y-intercept, or the point along the y-axis at which the line crosses.
In this case, the slope of the line, also known as the “rise over run”, is positive 2, indicating that the line rises from left to right. The y-intercept is positive 1, indicating that the line passes through the point (0, 1). Lines can always be easily graphed by forming an (x, y) table, substituting values of either x or y, and solving for the other variable. Once two points on the line are known, the line can be accurately graphed.
In this case, the slope of the line, also known as the “rise over run”, is positive 2, indicating that the line rises from left to right. The y-intercept is positive 1, indicating that the line passes through the point (0, 1). Lines can always be easily graphed by forming an (x, y) table, substituting values of either x or y, and solving for the other variable. Once two points on the line are known, the line can be accurately graphed.
Question 10 |
What is the probability of selecting a male from a group of 4 males and 8 females?
Question 10 Explanation:
The probability of an event taking place is the ratio of the number of successful events to the total number of possible events. In this case, a successful event is randomly selecting a male from the group. The total number of possible events is the number of people in the group. The ratio is then:
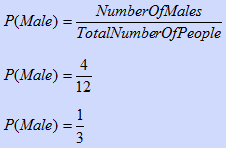
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 10 questions to complete.
|
List |
Next Test:
GED Math Practice Test 2 >>